
Оглавление Комбинаторика Методы Комбинаторики Комбинаторные задачи Уровни решения комбинаторных задач Правила суммы и произведения Примеры решения комбинаторных Задачи Комбинаторики Перечислительная комбинаторика Краткая историческая справка
Комбинаторика! (Комбинаторный анализ) — раздел математики , изучающий дискретные объекты, множества ( сочетания , перестановки , размещения и перечисления элементов) и отношения на них (например, частичного порядка ). Комбинаторика связана со многими другими областями математики — алгеброй , геометрией , теорией вероятностей , и имеет широкий спектр применения в различных областях знаний (например в генетике , информатике , статистической физике ). Термин «комбинаторика» был введён в математический обиход Лейбницем , который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». в оглавление
Комбинаторика. Основные формулы (перестановки, сочетания, размещения) и примеры решения задач.
Методы Комбинаторики Перестановкой из n элементов (например чисел 1,2,…, n ) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n . Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений. Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел. Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел. в оглавление
Комбинаторные задачи Комбинаторика – от латинского слова combinare , что означает «соединять, сочетать». Методы комбинаторики находят широкое применение в физике, химии, биологии, экономики и др. областях знания. Комбинаторику можно рассматривать как часть теории множеств – любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях. в оглавление
Уровни решения комбинаторных задач 1. Начальный уровень . Задачи поиска хотя бы одного решения, хотя бы одного расположения объектов, обладающих заданным свойствами — отыскание такого расположения десяти точек на пяти отрезках, при котором на каждом отрезке лежит по четыре точки; — такого расположения восьми ферзей на шахматной доске, при котором они не бьют друг друга. Иногда удаётся доказать, что данная задача не имеет решения (например, нельзя расположить 10 шаров в 9 урнах так, что бы в каждой урне было не более одного шара – хотя бы в одной урне окажется не менее двух шаров). в оглавление
2. Второй уровень . Если комбинаторная задача имеет несколько решений, то возникает вопрос о подсчете числа таких решений, описании всех решений данной задачи. 3. Третий уровень . Решения данной комбинаторной задачи отличаются друг от друга некоторыми параметрами. В этом случае возникает вопрос отыскания оптимального варианта решения такой задачи. Например: Путешественник хочет выехать из города А, посетить города В, С, и D . После чего вернуться в город А. в оглавление
Любимые коктейли знаменитых писателей
Правила суммы и произведения 1. Сколько различных коктейлей можно составить из четырёх напитков, смешивая их в равных количествах по два? AB, AC, AD, BC, BD, CD – всего 6 коктейлей 2. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3 ? Первой цифрой двузначного числа может одна из цифр 1, 2, 3 (цифра 0 не может быть первой). Если первая цифра выбрана, то вторая может быть любая из цифр 0, 1, 2, 3. Т.к. каждой выбранной первой соответствует четыре способа выбора второй, то всего имеется 4 + 4 + 4 = 4 · 3 = 12 различных двузначных чисел. А D С В в оглавление
Первая цифра вторая цифра 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 в оглавление
«Примеры решения комбинаторных задач: перебор вариантов, правило суммы, правило умножения». Сколькими способами могут быть расставлены 4 участниц финального забега на четырёх беговых дорожках? Р п = 4 · 3 · 2 · 1= 24 способа (перестановки из 4-х элементов) 1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3 3 4 2 4 2 3 4 3 4 2 3 2 3 4 1 4 3 1 4 3 4 1 1 3 2 4 1 4 1 2 4 2 4 1 2 1 2 3 1 3 1 2 3 2 3 1 2 1 1 дорожка 2 дорожка 3 дор . 4 дор . Р е ш е н о п е р е б о р о м в а р и а н т о в в оглавление
Пример Задачи Комбинаторики При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, таких, что сумма очков на верхних гранях равна двенадцати? Решение: Каждый возможный исход соответствует функции (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6+6 даёт нам нужный результат 12. Таким образом существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, такая, что сумма очков на верхних гранях равна двенадцати. в оглавление
Перечислительная комбинаторика Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок ) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п. Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения . Типичным примером задач данного раздела является подсчёт количества перестановок . Другой пример — известная Задача о письмах . в оглавление
Краткая историческая справка Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр ( Кардано , Гюйгенс, Паскаль, Ферма и другие в XVI—XVII вв.). Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654—1705).
Доказанная им теорема, получившая впоследствии название «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов. Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др. Новый, наиболее плодотворный период связан с именами П. Л. Чебышева (1821—1894) и его учеников А.А.Маркова(1856—1922) и А. М.Ляпунова (1857—1918).
В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. Н. Колмогоров, А. Я. Хинчин , Б. В. Гнеденко, Н. В. Смирнов и др.). В настоящее время ведущая роль в создании новых ветвей теории вероятностей также принадлежит советским математикам. в оглавление
Источник: nsportal.ru
Научный форум dxdy
Задача по комбинаторике (перебор неповторяющихся сочетаний)
Задача по комбинаторике (перебор неповторяющихся сочетаний)
23.04.2016, 02:13
Последний раз редактировалось zebracon 23.04.2016, 02:22, всего редактировалось 2 раз(а).
Помогите, пожалуйста, решить задачу.
Какое количество коктейлей можно сделать из N напитков? Условия: если присвоить числа напиткам, то коктейль 123,132,231 и тд — одно и тоже. Кол-во напитков в коктейле от 2 до N.
Сначала думал так:
Напиток может находиться в коктейле или нет, а значит находится, условно в двух состояних, а значит, кол-во коктейлей: 
Однако, т.к когда напиток только один — он не является коктейлем, то:
И когда нет ни одного напитка — это не коктейль:
Формула отлично подходит до 4 напитков, далее идет расхождение (для проверки можете использовать, что для 5 напитков 25 коктейлей, для 6 напитков 46 коктейлей — ручная проверка )
Re: Задача по комбинаторике (перебор неповторяющихся сочетаний)
23.04.2016, 02:24

А можно пример этой ручной проверки хотя бы для ?
Re: Задача по комбинаторике (перебор неповторяющихся сочетаний)
23.04.2016, 02:30
Последний раз редактировалось zebracon 23.04.2016, 02:31, всего редактировалось 1 раз.
Otta в сообщении #1117624 писал(а):

А можно пример этой ручной проверки хотя бы для ?
Источник: dxdy.ru
Презентация на тему Элементы комбинаторики 9 класс
Слайд 1Элементы комбинаторики
9 -11 классы, МБОУ Кочневская СОШ
учитель Грязнова
А.К

Слайд 2Основные вопросы:
Что такое комбинаторика?
Какие задачи считают комбинаторными?
Перестановки
Размещения
Сочетания

Слайд 3Не будем спорить — будем вычислять.
Г. Л е й б н и ц
Комбинаторика – радел математики, в котором рассматриваются задачи о подсчёте числа комбинаций составленных по определённым правилам.

Слайд 4II. Какие задачи считают комбинаторными?
Комбинаторные задачи
Задачи подсчёта числа комбинаций
из конечного числа элементов
Комбинаторика – от латинского слова combinare, что
означает «соединять, сочетать».
Методы комбинаторики находят широкое применение в физике, химии, биологии, экономики и др. областях знания.
Комбинаторику можно рассматривать как часть теории множеств – любую комбинаторную задачу можно свести к задаче о конечных множествах и их отображениях.

Слайд 5I. Уровни решения комбинаторных задач
1. Начальный уровень.
Задачи поиска
хотя бы одного решения, хотя бы одного расположения объектов, обладающих
заданным свойствами
— отыскание такого расположения десяти точек на пяти отрезках, при котором на каждом отрезке лежит по четыре точки;
— такого расположения восьми ферзей на шахматной доске, при котором они не бьют друг друга.
Иногда удаётся доказать, что данная задача не имеет решения
(например, нельзя расположить 10 шаров в 9 урнах так, что
бы в каждой урне было не более одного шара – хотя бы в
одной урне окажется не менее двух шаров).

Слайд 62. Второй уровень.
Если комбинаторная задача имеет несколько решений,
то возникает вопрос о подсчете числа таких решений, описании всех
решений данной задачи.
3. Третий уровень.
Решения данной комбинаторной задачи отличаются друг от друга некоторыми параметрами. В этом случае возникает вопрос отыскания оптимального варианта решения такой задачи.
Например:
Путешественник хочет выехать из города А, посетить города В, С, и D. После чего вернуться в город А.

Слайд 7На рис. изображена схема путей, связывающих эти города. Различные
варианты путешествий отличаются друг от друга порядком посещения городов В,
С, и .D. Существует шесть вариантов путешествия. В таблице указаны варианты и длин каждого пути:
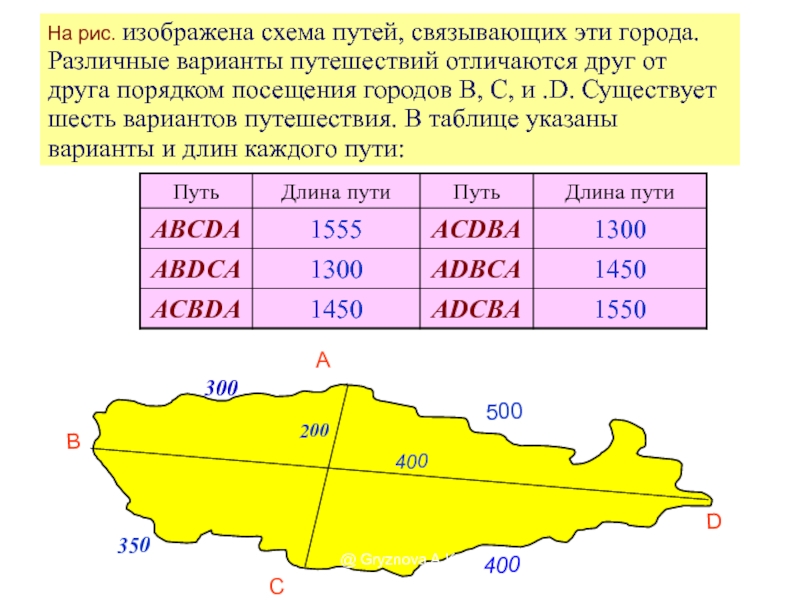
Слайд 8Комбинаторные задачи на оптимизацию приходится решать мастеру, стремящемуся к
быстрейшему выполнению задания, агроному, стремящемуся к наивысшей урожайности на данных
полях, и т.д.

Слайд 9Мы будем рассматривать лишь задачи о подсчёте числа решений
комбинаторной задачи.
Этот раздел комбинаторики, называемый теорией перечислений, тесно связан
с теорией вероятностей.

Слайд 10Правила суммы и произведения
1. Сколько различных коктейлей можно составить
из четырёх напитков, смешивая их в равных количествах по два?
AB, AC, AD, BC, BD, CD – всего 6 коктейлей
2. Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3 ?
Первой цифрой двузначного числа может одна из цифр 1, 2, 3 (цифра 0 не
может быть первой). Если первая цифра выбрана, то вторая может быть любая из
цифр 0, 1, 2, 3. Т.к. каждой выбранной первой соответствует четыре способа
выбора второй, то всего имеется
4 + 4 + 4 = 4·3 = 12 различных двузначных чисел.

Слайд 112. Сколько различных двузначных чисел можно составить из цифр
0, 1, 2, 3 ?
4 + 4 + 4 = 4·3 = 12 различных двузначных чисел.
Первая цифра вторая цифра
1
2
3

Слайд 12Правило произведения:
Если элемент А можно выбрать из множества элементов
п способами и для каждого такого выбора элемент В можно
выбрать т способами, то два элемента (пару) А и В можно выбрать п·т способами.

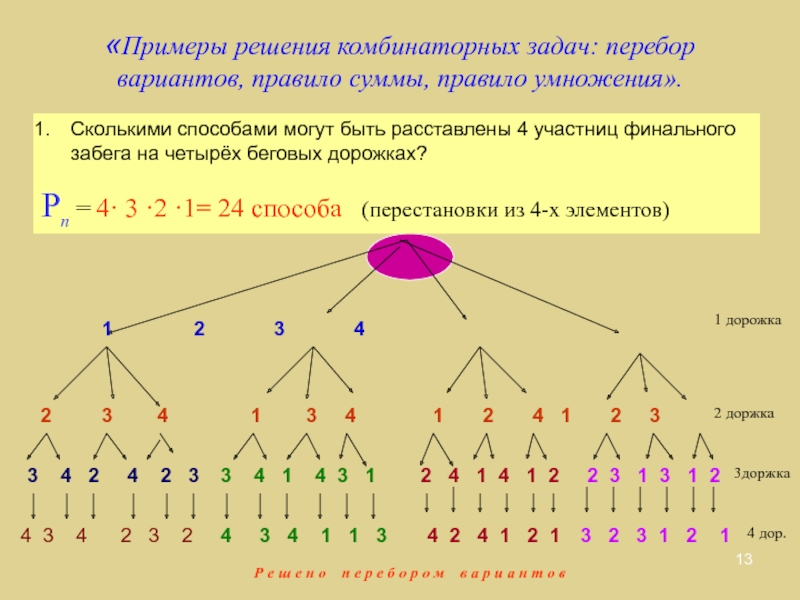
Слайд 13«Примеры решения комбинаторных задач: перебор вариантов, правило суммы, правило
умножения».
Сколькими способами могут быть расставлены 4 участниц финального забега на
четырёх беговых дорожках?
Рп = 4· 3 ·2 ·1= 24 способа (перестановки из 4-х элементов)
2 3 4 1 3 4 1 2 4 1 2 3
Р е ш е н о п е р е б о р о м в а р и а н т о в
Слайд 14II. Перестановки (1)
К в а р т е т
Проказница Мартышка,
Осёл,
Козёл
Да косолапый Мишка
Затеяли сыграть Квартет.
…………………………………………………….
Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой! — кричит Мартышка. –
Погодите!
Как музыке идти? Ведь вы не так сидите»
4·3·2·1 = 4! способов

Слайд 15II. Перестановки (2)
Перестановкой из п — элементов называется комбинации,
отличающиеся друг от друга лишь порядком следования элементов
Рп- число перестановок
(Р первая буква французского слова permutation- перестановка)
Рп= n·(n-1)·(n-2)·(n-3)·(n-4)·. . .·3 ·2 ·1= n!
Рп = n!
В математике принято считать 0! =1 и 1! = 1

Слайд 16Размещения (1)
Четыре попутчик решили обменяться визитными карточками. Сколько
всего карточек при этом было использовано?
получилось 12 карточек. Каждый из четырёх
попутчиков вручил визитку каждому из
трёх попутчиков
4 · 3 = 12
Комбинации, составленные из k элементов, взятых из n элементов, и отличающиеся друг от друга либо составом, либо порядком расположения элементов, называются размещениями из n элементов по k (0
Слайд 17Размещения (2)
Пуст имеется 4 шара и 3
пустых ячейки. Обозначим шары буквами a, b, c, d. В
пустые ячейки можно по разному разместить три шара из этого набора.
Выбирая по-разному первый, второй и третий шары, будем получать различные упорядоченные тройки шаров
Каждая упорядоченная тройка, которую можно составить из четырёх элементов называется размещением из четырёх элементов по три

Слайд 18Размещения (3)
Сколько же размещений можно составить из 4-х
элементов (abcd) по три?
abc abd
acb acd adb adc
bac bad bca bcd bda bdc
cab cad cba cbd cda cdb
dab dac dba dbc dca dcb
Р е ш е н о п е р е б о р о м в а р и а н т о в

Слайд 19Размещения (4)
Можно решить и не выписывая самих размещений:
первый
элемент можно выбрать четырьмя способами, так им может быть любой
элемент из четырёх;
для каждого первого второй можно выбрать тремя способами;
для каждых первых двух можно двумя способами выбрать третий элемент из двух оставшихся.
Получаем
Решено с использованием п р а в и л а у м н о ж е ни я

Слайд 20Сочетания
Сочетанием из п элементов по k называют любое множество,
составленное из k элементов, выбранных из п элементов
размещений в сочетаниях не имеет значение порядок элементов. Два сочетания отличаются друг от друга хотя бы одним элементом

Слайд 21Р е ш и з а д а
ч и:
1. На плоскости отмечено 5 точек.
Сколько получится отрезков, если соединить точки попарно?
2. На окружности отмечено п точек. Сколько существует треугольников с вершинами в этих точках?

Слайд 22Источники информации
В.Ф.Бутузов, Ю.М.Колягин, Г.Л. Луканкин, Э.Г.Позняк и др. «Математика»
учебное пособие для 11кл общеобразовательных учреждений /рекомендовано Министерством образования РФ/
М., Просвещение, 1996.
Е.А. Бунимович, В.А. Булычёв: «Вероятность и статистика», пособие для общеобразовательных учебных заведений 5 – 9 классы / допущено Министерством образования Российской Федерации // Дрофа Москва 2002
Ю.Н. Макарычев, Н.Г.Миндюк «Алгебра: элементы статистики и теории вероятностей 7 – 9 классы» Под редакцией С.А.Теляковского М: Просвещение , 2006 г
Треугольнички http://works.doklad.ru/images/_E3ZV-_wFwU/md87b96f.gif
Остальные рисунки созданы Грязновой А.К.
Источник: theslide.ru
